Ingenuity and reasoning are indispensable tools for solving exercises in the Mexican Mathematics Olympiad.
The Mexican Mathematics Olympiad is an annual competition for pre-university students. A considerable number of math problems similar to those solved by contestants have been designed and documented. Ingenuity and reasoning are indispensable tools for solving these exercises. The type of problems defined for this competition are the key to discovering talented students, who can set in motion the complex machinery of knowledge, ability, and imagination to solve similar problems with only a theoretical basis.
At Tec de Monterrey’s High School, Campus Aguascalientes, we have undertaken the task of identifying and supporting mathematically gifted students. Our goal is to give any students, who so wish, the opportunity to participate in this program created by the Mexican Mathematical Society (SMM).
“These students can set in motion the complex machinery of knowledge, ability, and imagination to solve math problems with only a theoretical basis.”
In addition to class time, space has been developed where students can discover, generate non-standardized ideas and deepen their knowledge of mathematics.
In the first two semesters of high school, the nature of the topics addressed is reduced to acquiring knowledge and handling formulae to be applied to relatively simple problems. Students learn the terminology and theoretical concepts and complete reinforcement exercises. Moreover, students, who so decide, can devote additional time to solving Olympiad-type problems during class or at home, fully aware that these exercises are not compulsory.
“As teachers, we encourage every student to face these challenges and then we can discover mathematical talent in the solution of the same.”
The following is an example of how we approach these theory-based and Olympiad-type exercises during class.
Exercises that serve as a theoretical basis
The topic “laws of exponents” requires the understanding, memorization, and mechanization of such laws. Students can investigate the laws of exponents, complete the table and then perform the mechanization exercises, either individually or collaboratively.
Traditional exercise for the laws of exponents
-
With your knowledge of the laws of exponents, relate both columns.
2. Traditional exercise for the application of the laws of exponents.
Olympiad-type exercises for the laws of exponents
After completing the exercises that serve as a theoretical basis, students then face the challenges, which are merely the Olympiad-type exercises. The solution to these exercises can be reached in a variety of ways. It must be noted that no more than two or three exercises can be seen in each class since it takes much longer to solve them than mechanization problems.
These challenges are not mandatory, unlike the pre-challenge activities. Whoever wants to solve them can do so, and it is precisely the talented students who take on the challenge, which does not necessarily mean those who have outstanding grades. As teachers, we encourage every student to face these challenges and then we can discover mathematical talent in the solution of the same.
For the past four years, we have been implementing the challenges as part of the class sessions with first-semester students, achieving satisfactory results. We have 15 students participating in the different stages of the Mexican Mathematical Olympiad and, in the last two years, two of our students have won a bronze medal in the national competition.
What do you need to work in the classroom on Olympiad-type problems?
You merely need to select problems from the mathematics calendars and adapt them to the topics included in your curriculum. At times, some of the problems might not seem to be useful for the subject, which is where teachers’ ingenuity to adapt them to their needs comes into play. They could be part of a sort of riddle that many students would enjoy solving. For example:
Real Numbers: adaptation of an Olympiad-type problem
I want to invite all teachers to explore these exercises and their in-class application, as a tool to discover our students’ talent and encourage them to study this area of knowledge in greater depth.
About the author
Sandra Lilia Castillo Flores (sandra.castillo@tec.mx) is an Electrical and Mechanical Engineer. She is currently a teacher in the Science Department at Tec de Moterrey’s High School, Campus Aguascalientes, and Mexican Mathematics Olympiad coach in the same city.
References
García L., Pérez M. y Raggi M. (2017). Matemáticas naturales. Escuela Nacional de Estudios Superiores, Unidad Morelia.
This article from Observatory of the Institute for the Future of Education may be shared under the terms of the license CC BY-NC-SA 4.0 
)
)

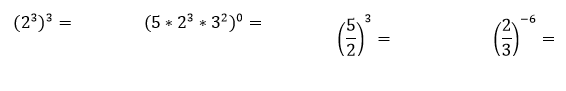











)
Sofía García-Bullé
Sofía García-Bullé
Sofía García-Bullé